Day 1 review presentation and alternative compressed form.
Proof of Lagrange's Trig Identity
Mathematica notebook illustrating some complex function graphing techniques.
Click here for that silly cube root applet. (Or here for an updated three.js version.) Then drag out a path with your mouse. Your browser must support Java for the old version to work.
Let $\mathcal{D}_{a,b,\theta} = \{z\in \mathbb{C} : a < |z| < b \mbox{ and } -\theta < Arg(z) < \theta \}$. Given $0\leq a < b$ and $\theta \in (0,\pi]$, the set ${\mathcal D}_{a,b,\theta}$ is a domain in ${\mathbb{C}}$ which supports precisely three continuous complex-valued cube root functions. None of these cube root functions, however, can be extended continuously to the annulus $\{z\in\mathbb{C}: a < |z| < b\}$. The animation below illustrates the continuous cube root functions defined on ${\mathcal D}_{\frac{1}{2},\frac{3}{2},\theta}$ for increasing values of $\theta$. (Notice that the roles played by $a$ and $b$ are not particularly interesting. You might as well take $a=0$ and $b=\infty$... but with $b=\infty$ the plot extends outside any frame.)
A neighborhood of -1 and its image under a cube root map which is discontinous on the negative reals:
An illustration of the Riemann surface of the cube root (courtesy of Wikipedia).
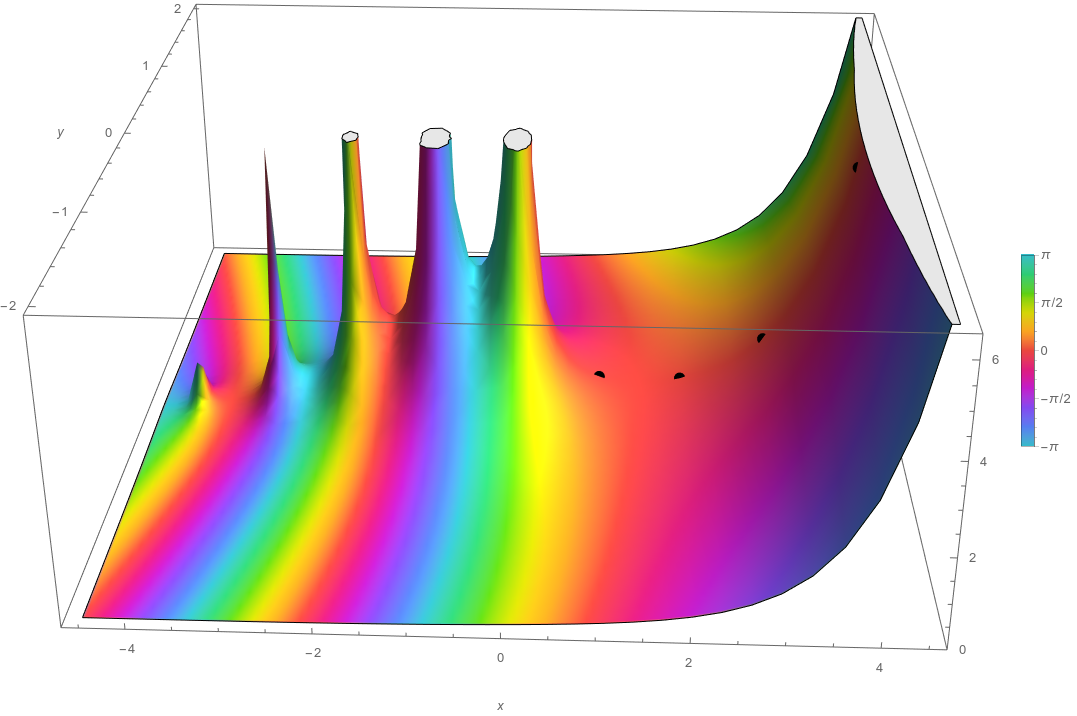
Black dots correspond to positive integer inputs.
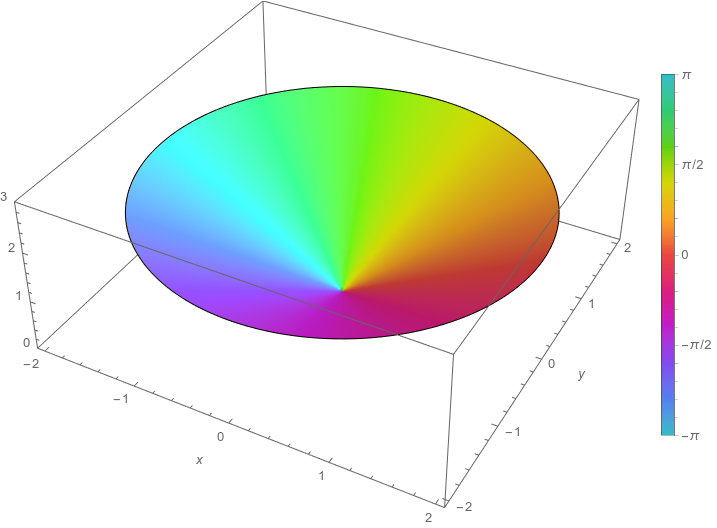
Elliptic Möbius transformations
Hyperbolic Möbius transformations
Parabolic Möbius transformations
Graphs and contour plots of solutions to example boundary value problems discussed in class:
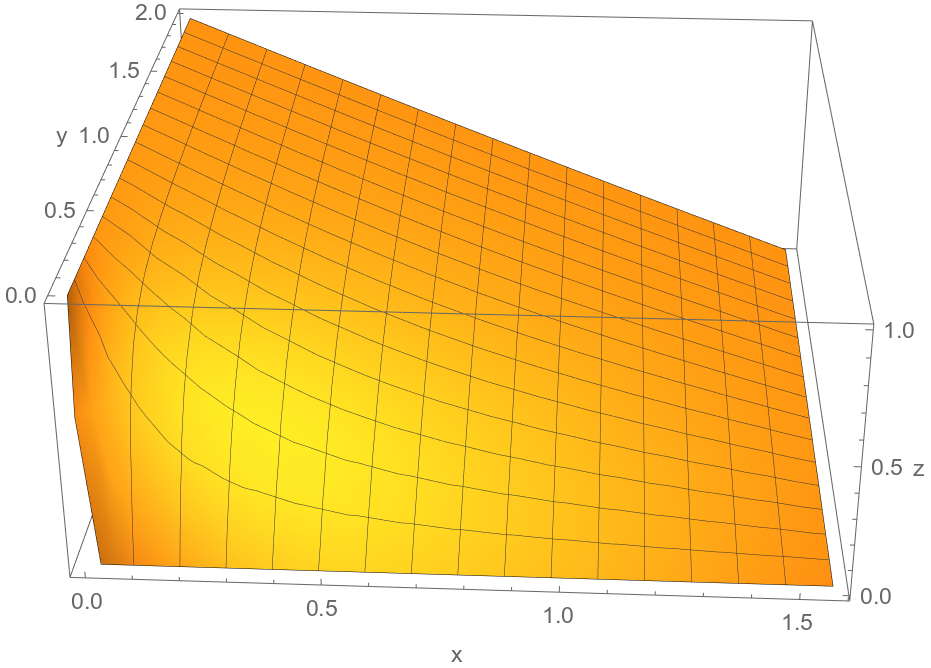
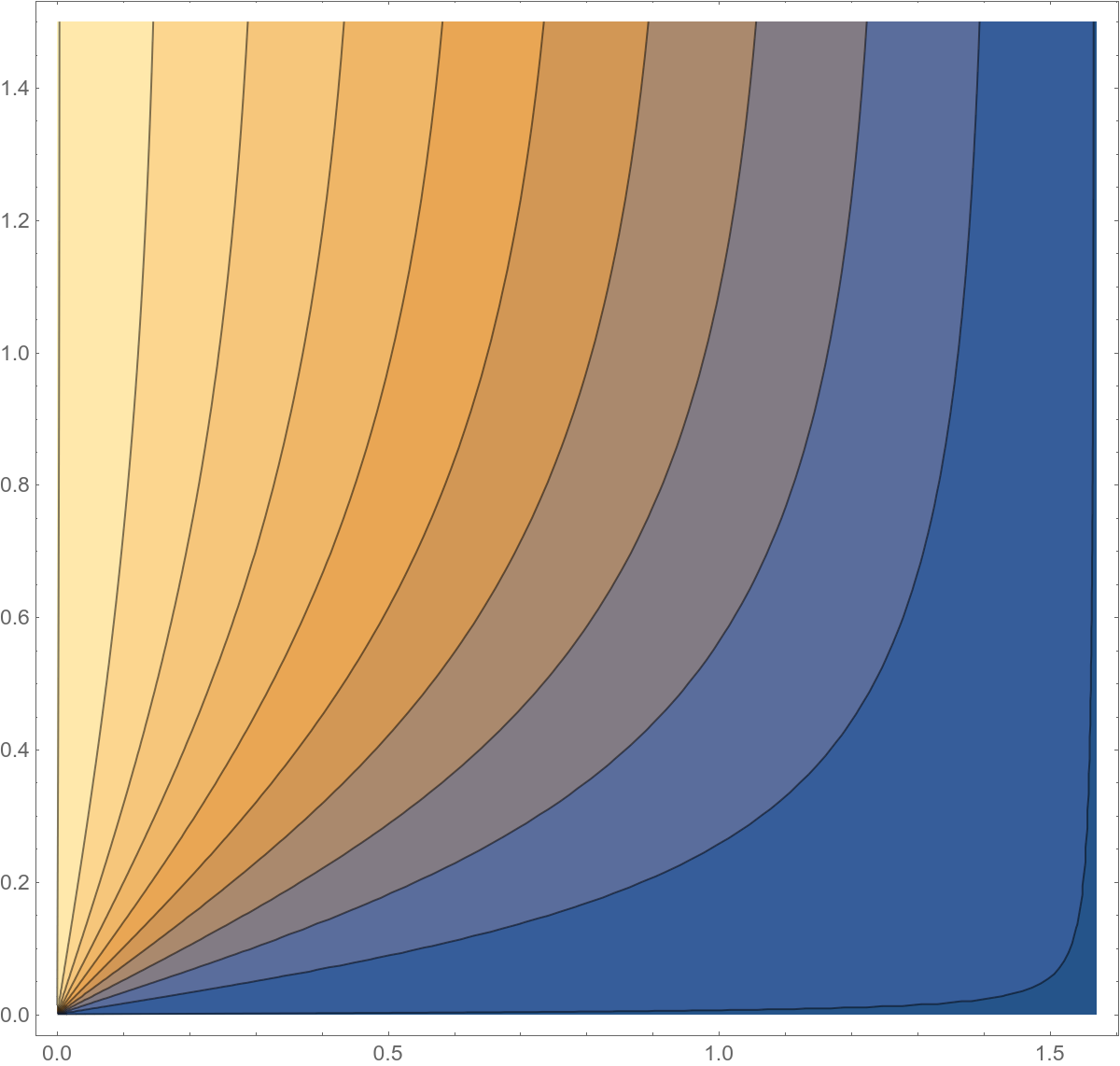
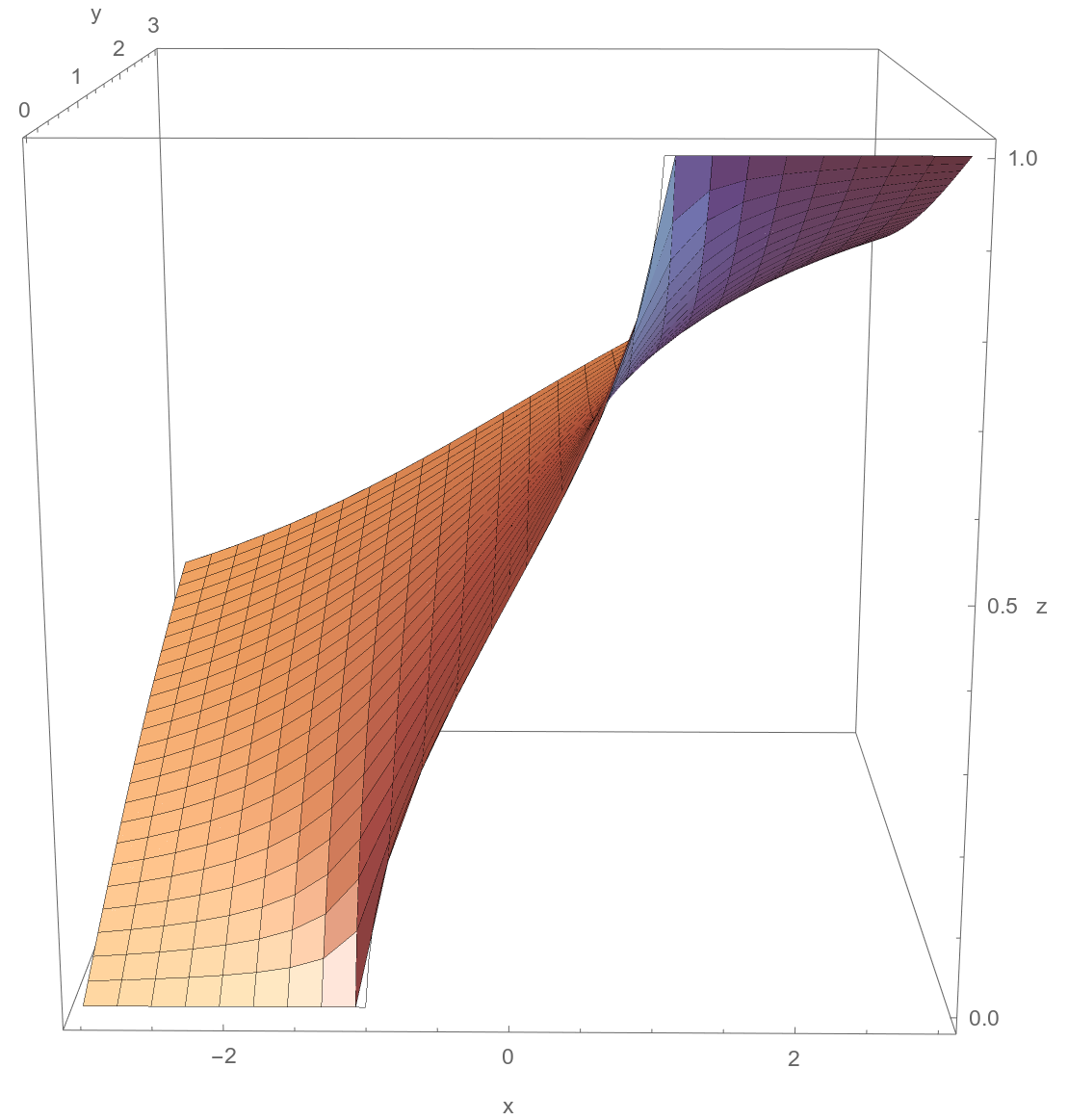
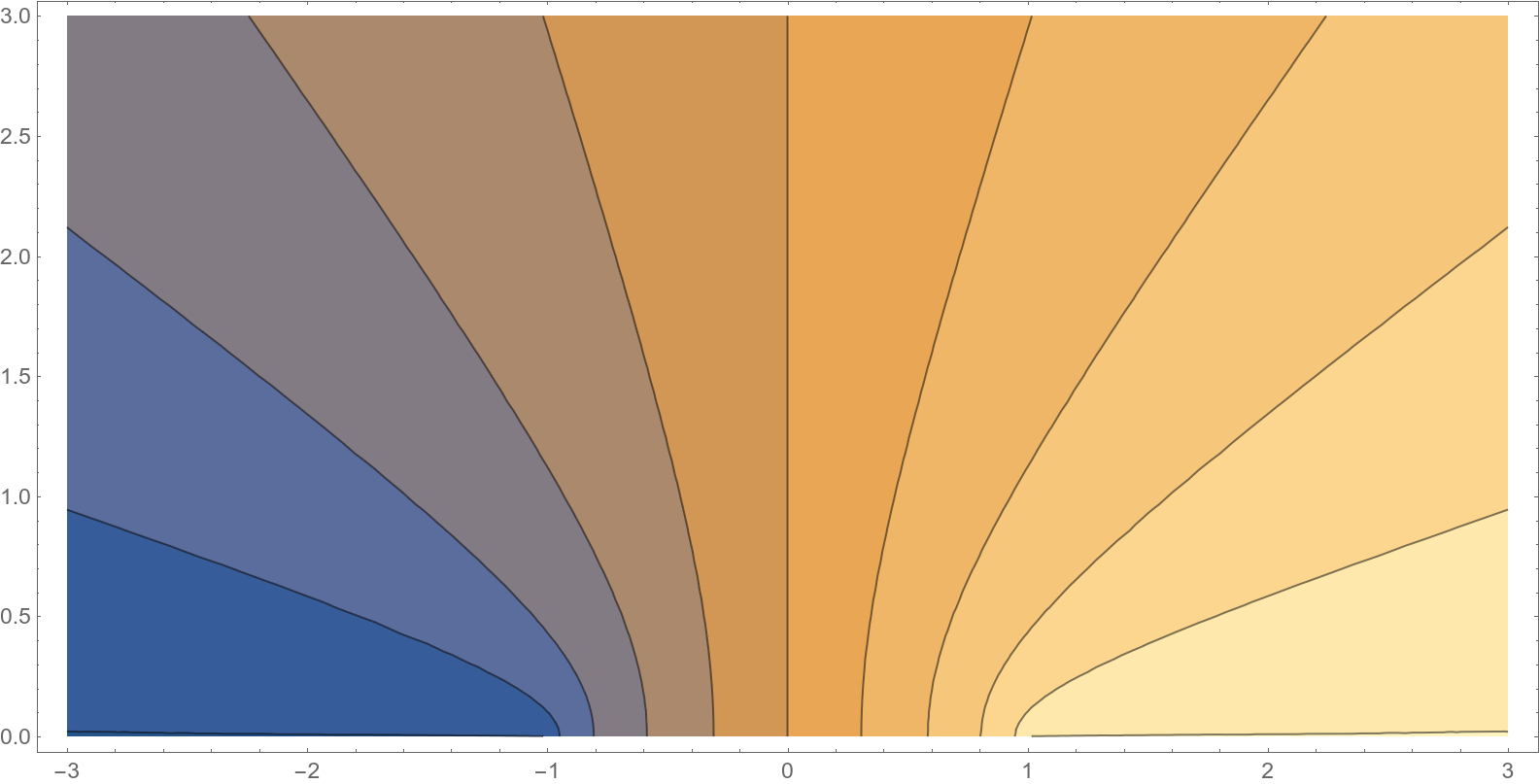
Basic properties of Möbius transformations.
Mathematica notebook illustrating a brute force proof that conformal changes of coordinates preserve harmonicity.
Winding number example, computer graphics perspective.
