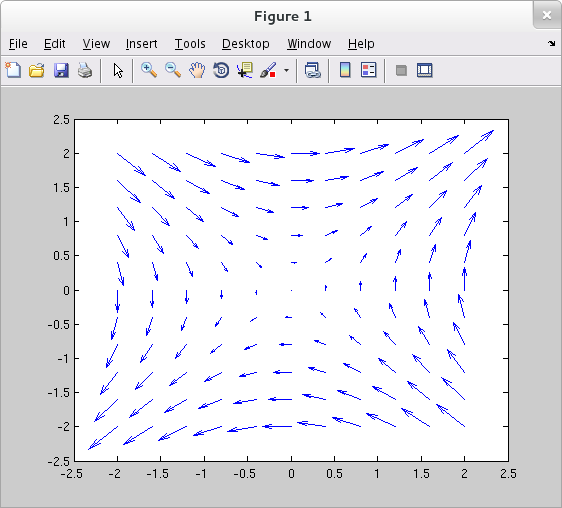
The following Matlab code generates a graphical representation of the planar vector field ${\bf F}(x,y)=y\,{\hat {\bf \unicode{x0131}}} + x\,{\hat {\bf \unicode{x0237}}}$.
>> x = -2:.4:2; >> y = -2:.4:2; >> [x,y] = meshgrid(x,y); >> quiver(x,y,y,x)

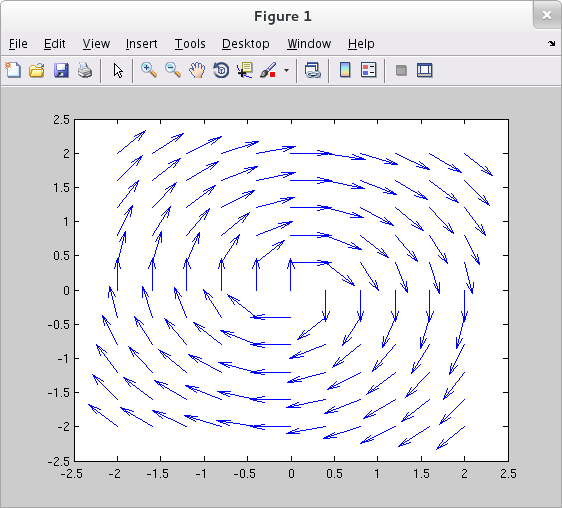
Another example: ${\bf F}(x,y)=\frac{y}{\sqrt{x^2+y^2}}\,{\hat {\bf \unicode{x0131}}} + \frac{-x}{\sqrt{x^2+y^2}}\,{\hat {\bf \unicode{x0237}}}$.
>> x = -2:.39999:2; >> y = -2:.4:2; >> [x,y] = meshgrid(x,y); >> M = y./sqrt(x.^2 + y.^2); >> N = -x./sqrt(x.^2 + y.^2); >> quiver(x,y,M,N)
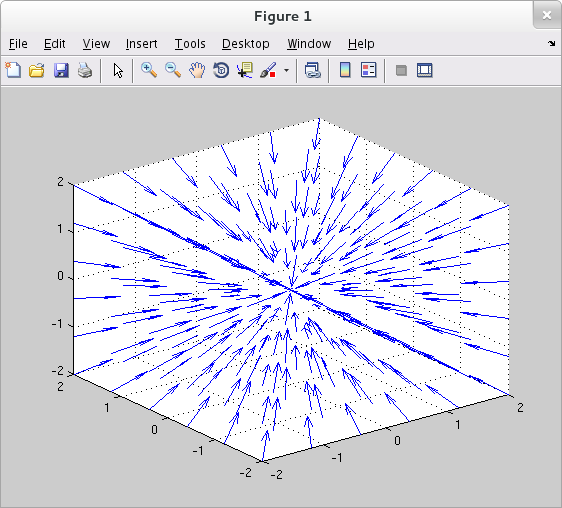
A space vector field example: ${\bf F}(x,y,z)=\frac{-x}{\sqrt{x^2+y^2+z^2}}\,{\hat {\bf \unicode{x0131}}} + \frac{-y}{\sqrt{x^2+y^2+z^2}}\,{\hat {\bf \unicode{x0237}}} + \frac{-z}{\sqrt{x^2+y^2+z^2}}\,{\hat {\bf k}}$.
>> x = -2:.8:2; >> y = -2:.8:2; >> z = -2:.8:2; >> [x,y,z] = meshgrid(x,y,z); >> M = -x./sqrt(x.^2 + y.^2 + z.^2); >> N = -y./sqrt(x.^2 + y.^2 + z.^2); >> P = -z./sqrt(x.^2 + y.^2 + z.^2); >> quiver3(x,y,z,M,N,P)