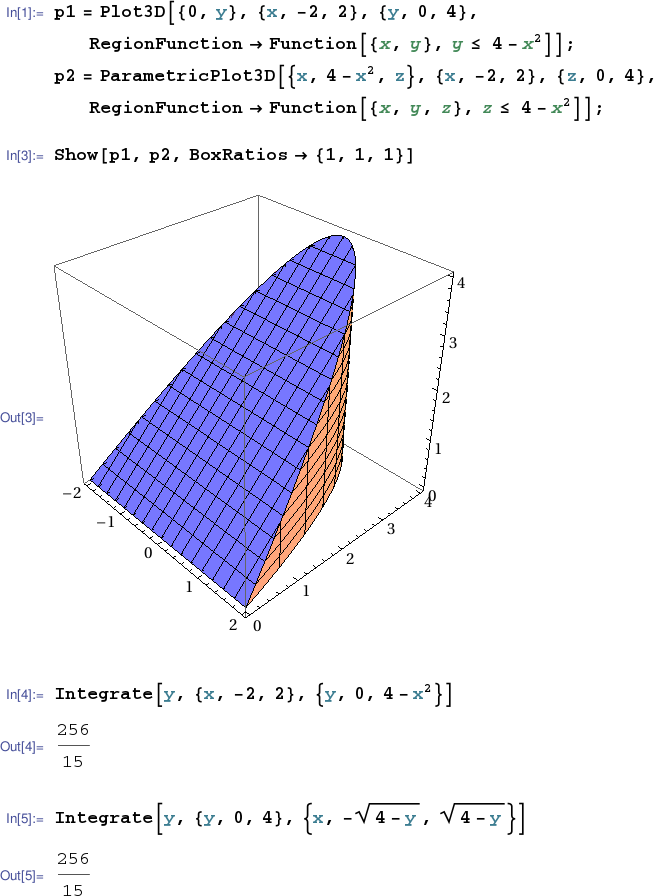
The Mathematica notebook below illustrates the computation of the volume of the solid below the plane $z=y$ and above the region $R$ in the $xy$-plane between the $x$-axis and the parabola $y=4-x^2$ using iterated integrals.

The same computation using MATLAB's symbolic toolkit:
>> syms x y >> int(int(y,y,0,4-x^2),x,-2,2) ans = 256/15 >> int(int(y,x,-sqrt(4-y),sqrt(4-y)),y,0,4) ans = 256/15
And now numerically...
>> integral2( @(x,y) y, -2, 2, 0, @(x) 4-x.^2 ) ans = 17.0667 >> integral2( @(y,x) y, 0, 4, @(y) -sqrt(4-y), @(y) sqrt(4-y) ) ans = 17.0667