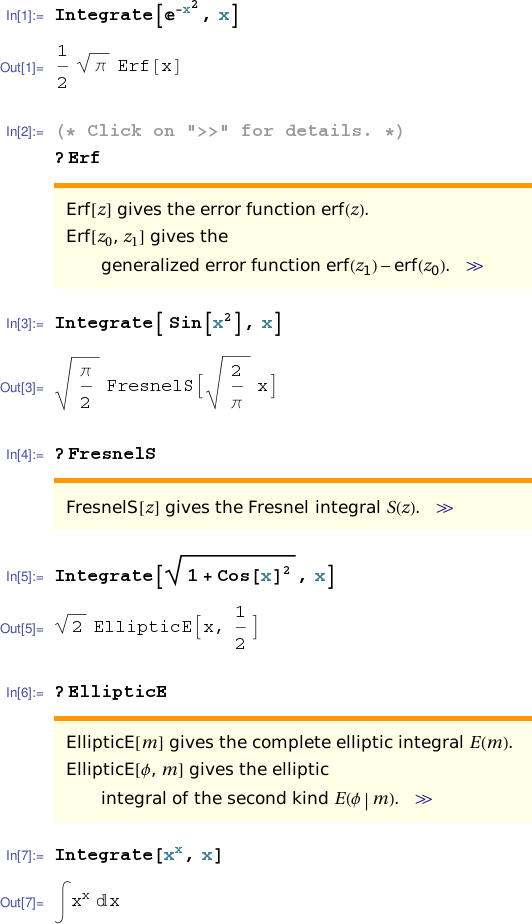
While the derivative of an elementary function is always elementary, often the antiderivatives of an elementary function fail to be elementary. So what happens if you ask a CAS to find an antiderivative of $f(x)$ when no elementary antiderivative exists for $f(x)$? Sometimes the system will do nothing but spit the expression $\int f(x) dx$ back at you. But in many cases you'll find the system has a name for a (non-elementary) antiderivative of $f(x)$, or that the system through some substitution can relate an antiderivative of $f(x)$ to some named non-elementary function. This page offers a few examples.
>> syms x >> int( exp(-x^2) ) ans = (pi^(1/2)*erf(x))/2 >> int( sin(x^2) ) ans = (2^(1/2)*pi^(1/2)*fresnelS((2^(1/2)*x)/pi^(1/2)))/2 >> int( sqrt( 1+cos(x)^2 ) ) ans = 2^(1/2)*ellipticE(x, 1/2)
The definitions of erf (the error function),
fresnelS (the Fresnel integral $S$) and ellipticE
(the elliptic integral of the second kind)
are
${\displaystyle erf(x) = \frac{2}{\sqrt{\pi}}\int_0^x e^{-t^2}\,dt}$,
${\displaystyle frenelS(x) = \int_0^x \sin{\frac{\pi t^2}{2}}\,dt}$ and
${\displaystyle ellipticE(x,m) = \int_0^x \sqrt{1-m\sin{t}^2}\,dt}$ (for $\frac{-\pi}{2}< x<\frac{\pi}{2}$).
So in the examples above the MATLAB symbolic toolbox has merely transformed
the integrals we wished to compute into closed related (named) integrals.
In the next example, MATLAB just throws the indefinite integral back at us.
>> int( x^x ) Warning: Explicit integral could not be found. ans = int(x^x, x)
