Suppose $f(x)$ and $g(x)$ are positive for sufficiently large values of $x$. We say $f$ grows faster than $g$ as $x\rightarrow\infty$ if ${\displaystyle \lim_{x\rightarrow\infty}\frac{f(x)}{g(x)}=\infty}$. We say $f$ and $g$ grow at the same rate as $x\rightarrow\infty$ if ${\displaystyle \lim_{x\rightarrow\infty}\frac{f(x)}{g(x)}=L}$ for some positive, finite value $L$.
This page uses symbolic limit computation to compare rates of growth for a few pairs of functions.
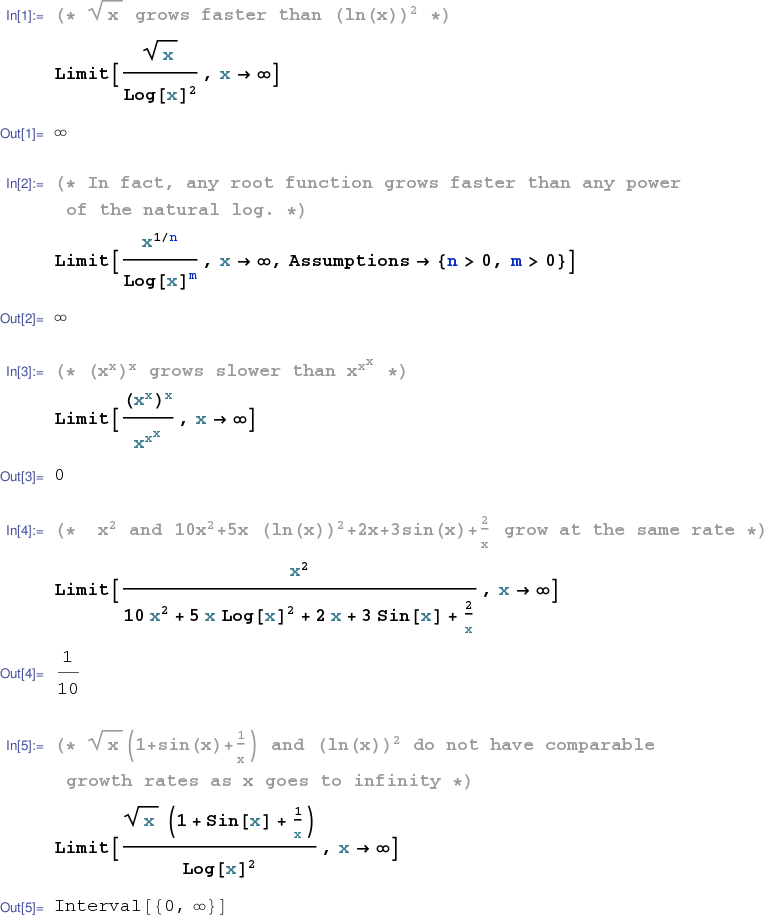
The expression $\sqrt{x}$ grows faster than $(\ln{x})^2$ (as $x\rightarrow\infty$).
>> syms x f g >> f=sqrt(x); g=log(x)^2; >> limit( f/g, x, inf ) ans = Inf
The example above may be generalized. Any root function grows faster than any power of the natural log function.
>> syms x f g >> syms n m positive >> f = x^(1/n); g = log(x)^m; >> limit( f/g, x, inf ) ans = Inf
The exponential expression $(x^x)^x$ grows slower than the power tower $x^{(x^x)}$.
(Incidentally MATLAB, in defiance of long-standing mathematical convention,
treats ^ as left-associative. So use parentheses
when building power towers!)
>> syms x f g >> f=(x^x)^x; g=x^(x^x); >> limit( f/g, x, inf ) ans = 0
The expressions $x^2$ and $10x^2+5x(\ln{x})^2+2x+3\sin{x}+\frac{2}{x}$ grow at the same rate (as $x\rightarrow\infty$).
>> syms x f g >> f=x^2; g=10*x^2+5*x*log(x)^2 + 2*x + 3*sin(x) + 2/x; >> limit( f/g, x, inf ) ans = 1/10
MATLAB balks at the following attempt to compare the growth rates of $\sqrt{x}(1+\sin{x}+\frac{1}{x})$ and $(\ln{x})^2$ as $x\rightarrow\infty$. (See the Mathematica notebook session below.)
>> syms x f g >> f=sqrt(x)*(1+sin(x)+1/x); g=log(x)^2; >> limit( f/g, x, inf ) ans = limit((x^(1/2)*(sin(x) + 1/x + 1))/log(x)^2, x == Inf)
