MATLAB's symbolic toolbox contains a method finverse() for finding functional inverses.
>> syms x >> f(x) = cos(sqrt(x+1)); >> g = finverse( f ) g(x) = acos(x)^2 - 1 >> simplify( compose(g,f,x), 'IgnoreAnalyticConstraints', true ) ans = x >> simplify( compose(f,g,x), 'IgnoreAnalyticConstraints', true ) ans = x
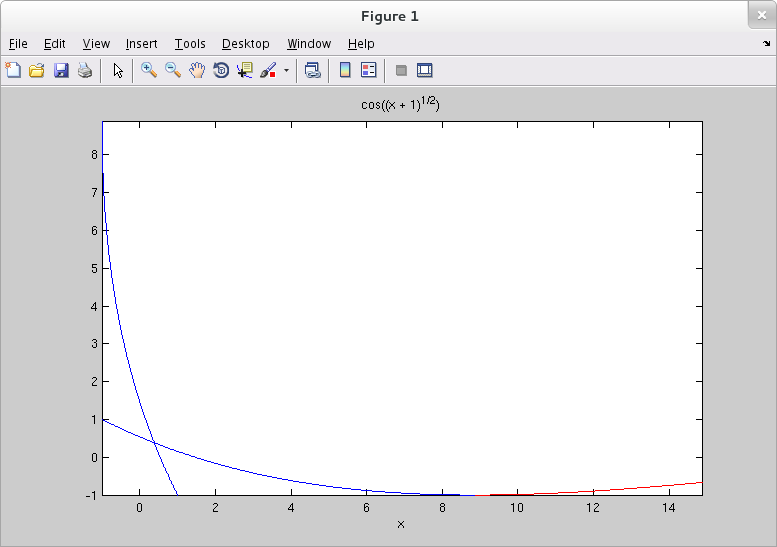
Notice that you need to pay attention to domains and ranges. The function $f$ in the example above is defined for all values in $[-1,\infty)$, but is not one-to-one. The function returned by finverse() is the inverse of the restriction of $f$ to $[-1,\pi^2-1]$.
>> ezplot( g, [-1 1] ); >> hold on >> ezplot( f, [-1 pi^2-1] ) >> axis equal >> h = ezplot( f, [pi^2-1 pi^2+5] ); >> set(h, 'Color', 'r') >> xlim([-1 pi^2+5]) >> ylim([-1 pi^2-1])

The command InverseFunction[] may be used to find functional inverses.
