
This page includes implementations in MATLAB and Mathematica of Newton's method for approximating zeros. The Mathematica section also includes an implementation of the bisection method. The Sage section presents an interact which illustrates Newton's method graphically.
The following implementation of Newton's method (newtonsMethod.m) illustrates the while loop structure in MATLAB which causes a block of code to be executed repeatedly until a condition is met.
function approximateZero = newtonsMethod( fnc, x0, tol ) % implementation of Newton's Method for finding a zero of a function % requires a symbolic expression, a starting point, and a tolerance as input % produces either an input, which when substituted into the given expression, % yields an output with absolute value less than the specified tolerance, % or a warning message indicated that the tolerance has not been met. % Author: R Smyth % Version: 1.0 8/11/2013 % Since convergence is not guaranteed for Newton's method, % set a maximum number of iterations. % Of course we could have let the user control this parameter. maxNumIter = 20; itCounter = 0; % Initialize iteration counter. syms fp; % derivative fp = diff(fnc); xcur = x0; while ( (abs(subs(fnc,xcur))>tol) & (itCounter < maxNumIter) ) xcur = double(xcur - subs(fnc,xcur)/subs(fp,xcur)); itCounter = itCounter+1; end if( abs(subs(fnc,xcur))>tol ) disp(['Warning: Tolerance not met after ' num2str(maxNumIter) ' iterations.']); end approximateZero = xcur;
Let's try it out from the command window.
>> syms x >> newtonsMethod(x^3-x-1,2,.0001) ans = 1.3247 >> newtonsMethod(sqrt(abs(x)),1,.01) Warning: Tolerance not met after 20 iterations. ans = 1
Thanks to the Intermediate Value Theorem we know that if function $f$ is continuous on interval $[a,b]$ and produces values of opposite sign at the endpoints $a$ and $b$, then $f$ must have a zero somewhere in the interval. If we evaluate $f$ at the midpoint $\frac{a+b}{2}$, either the sign agrees with the sign of $f(a)$, in which case $f$ surely has a zero in $[\frac{a+b}{2},b]$, or the sign does not agree, in which case $f$ surely has a zero in $[a,\frac{a+b}{2}]$. Either way, we've found an interval of half the length of our original interval which still surely contains a zero of $f$. The bisection method merely starts with an interval $[a,b]$ as above and iterates this [evaluate]-[test sign]-[bisect interval] step until the location of a zero of $f$ has been found with sufficient precision.
The Mathematica session below uses the bisection method to approximate a zero of $2\sin{x}-x$ in the interval $[\frac{8}{5},2]$. (In other words a solution of $2\sin{x}=x$ is approximated.) The nextBisection[] function performs the key step of the bisection method. It accepts an interval and returns either the right half or the left half of the interval, depending on whether the sign of $f$ at the midpoint agrees with the sign of $f$ at the lower endpoint. (Notice that testing the sign of the product is a quick and dirty way to test for sign agreement.) The Nest[] command provides a convenient method for applying a function iteratively. Nest[] accepts a function, an initial input, and a number specifying how many times to apply the function. For example Nest[ Blah, 7, 3 ] produces Blah[Blah[Blah[7]]]. The NestList[] variant is the same except it returns a list containing all the intermediate iterates as well as the final one.

Convergence of the bisection method is relatively slow, but foolproof.
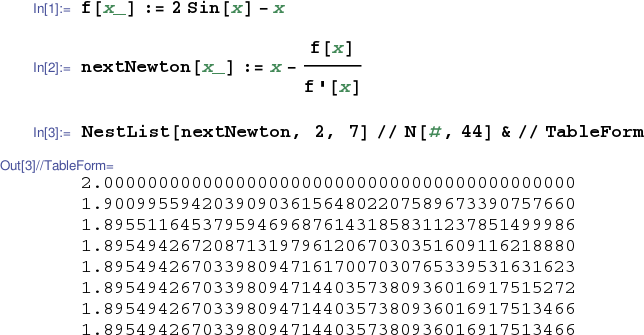
Below we implement the iterative step of Newton's method as nextNewton[]. We then again use Mathematica's NestList[] command to apply nextNewton[] iteratively to the function $x \mapsto 2\sin{x}-x$ (with starting value $x=2$). Although, as in this example, the rate of convergence of convergence of Newton's method is typically far more impressive than the rate of convergence of the bisection method, you should be aware that Newton's method is not guaranteed to converge. (See the text.)
A slightly more sophisticated implementation would, rather than using a predetermined number of iterations, continue iterating until the output of $f$ was within a specified tolerance of zero.