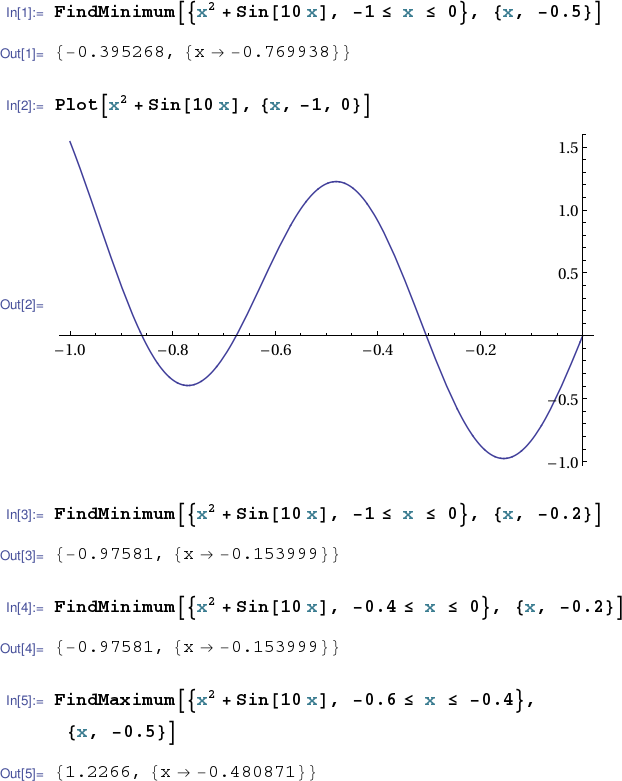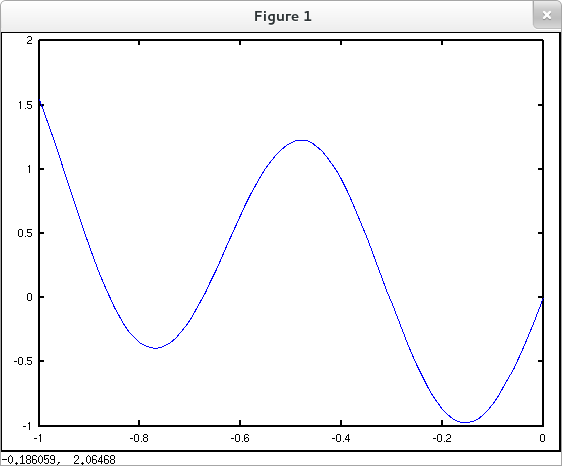
This page does not walk through the standard calculus procedure for finding local extrema in any of our CASs. (If you've followed this TechCompanion this far you should already be able to do so.) Rather this page presents convenience methods for finding local extreme values in each of our target CASs.
The command fminbnd() finds the location of a local minimum of a continuous function (specified via a function handle) on a given interval.
octave:1> f = @(x) x.^2 + sin(10*x); octave:2> fminbnd(f,-1,0) ans = -0.76994 octave:3> x = -1:.01:0; octave:4> y = f(x); octave:5> plot(x,y)

In the example above we can see from the plot that our call to fminbnd() has returned an approximation to an input where a local minimum of $x^2+\sin{10x}$ occurs, but that the local min it has found is not the global min over the specified interval $[-1,0]$. Using the plot as a guide, we can make two calls to fminbnd() specifying appropriate intervals to find both the local min on the left and the global min as well. Furthermore, if we allot two output variables, fminbnd() will return the approximate values of the local min's as well as their input locations.
octave:6> [x ymin] = fminbnd(f,-1,-0.6) x = -0.76994 ymin = -0.39527 octave:7> [x ymin] = fminbnd(f,-0.4,0) x = -0.15400 ymin = -0.97581
Finally we can locate the interior local maximum of $f(x)=x^2+\sin{10x}$ by passing fminbnd() a handle to $-f(x)$ (and an appropriate interval).
octave:8> g = @(x) -f(x); octave:9> [x y] = fminbnd(g, -0.6, -0.3) x = -0.48087 y = -1.2266
Of course an input that yields a local min of $-f(x)$ yields a local max of $f(x)$. But the value of $-f(x)$ there is the negative of the value of $f(x)$. So in the example above the local max of $x^2+\sin{10x}$ occurring approximately at $x=-0.48087$ has a value of about $+1.2266$.
The command FindMinimum[] accepts a one variable expression, an interval and a search starting point. It returns both the value and location of a local min of the given expression on the given interval. It's not guaranteed to find the global min over the given interval. Plotting the expression in question can often guide a choice of starting point (or better yet, choice of subinterval) to find a particular local min. Mathematica also offers a corresponding FindMaximum[] method.