Each of our target CASs is capable of symbolic differentiation. This page introduces this feature for each CAS.
In MATLAB (or Octave) polynomials (encoded as row vectors of coefficients) may be differentiated with the polyder() method. For instance,
octave:1> polyder( [ 4 1 0 3 ] ) ans = 12 2 0
shows that ${\displaystyle \frac{d}{dx}\left(4x^3+x^2+3\right) = 12x^2+2x}$ -- a result that can easily can be verified by hand.
The Symbolic toolbox method diff(), however, is a much more powerful and versatile tool for performing symbolic differentiation. This method may be used to differentiate sums, differences, products, quotients, roots and compositions of a host of functions including all the familiar trig functions, logarithmns and exponential functions. (The Symbolic toolbox method diff() is not to be confused with the arithmetic operator diff() introduced earlier for computing differences between consecutive elements in numerical arrays. In MATLAB, diff() is a so-called "overloaded" method. The system determines which method to invoke based on the argument(s) in the call. If you pass diff() a symbolic expression, then the Symbolic toolbox diff() method will be used.)
The following MATLAB session illustrates diff().
>> diff( [ 2 0 5 9 ] ) % Arithmetic diff operator. ans = -2 5 4 >> syms x y >> diff( x^3 ) % Symbolic toolbox differentiation. ans = 3*x^2 >> diff( (sqrt(x) - 3)/(sqrt(x) + 1) ) ans = 1/(2*x^(1/2)*(x^(1/2) + 1)) - (x^(1/2) - 3)/(2*x^(1/2)*(x^(1/2) + 1)^2) >> diff( 4*x^3 + x^2 + 3 ) ans = 12*x^2 + 2*x >> y = (2*x-7)^(-3) + 1/x y = 1/(2*x - 7)^3 + 1/x >> diff( y ) ans = - 6/(2*x - 7)^4 - 1/x^2
Notice that symbolic expressions in MATLAB do not employ
the componentwise operators
.*,
.^ and
./ which were so prevalent in our
earlier numerical work in Octave/MATLAB.
This can be a nuisance.
You can, however, convert a symbolic expression to MATLAB's "ordinary"
syntax with the matlabFunction() command.
>> syms x y >> y = 1/(1+x^2); >> yp = diff(y) yp = -(2*x)/(x^2 + 1)^2 >> matlabFunction(yp) ans = @(x)x.*1.0./(x.^2+1.0).^2.*-2.0
Of course the Symbolic toolbox method diff() can be applied repeatedly to compute higher order derivatives, but it also admits an optional input specifying the order of differentiation.
>> syms x >> diff( diff( diff( x^5 ) ) ) ans = 60*x^2 >> diff( x^5, 3 ) ans = 60*x^2 >> diff( 1/(x^2+1) , 11 ) % A computation which would be straightforward, but quite tedious by hand. ans = (479001600*x)/(x^2 + 1)^7 - (11176704000*x^3)/(x^2 + 1)^8 + (71530905600*x^5)/(x^2 + 1)^9 - (183936614400*x^7)/(x^2 + 1)^10 + (204374016000*x^9)/(x^2 + 1)^11 - (81749606400*x^11)/(x^2 + 1)^12
Sometimes you need to specify explicitly the variable with respect to which you want differentiation to be performed.
>> syms a x >> diff( x*a^2 ) % MATLAB treats 'a' as a fixed parameter and 'x' as a variable. ans = a^2 >> diff( x*a^2, a ) % This forces MATLAB to treat 'a' as the variable of differentiation. ans = 2*a*x
You can require MATLAB to treat certain symbols as functions of others without providing an explicit formula for the functional dependence.
>> syms x n f(x) g(x) >> diff( f(x)*g(x) ) % MATLAB can apply the product rule, but can't differentiate the factors f(x) and g(x) since we haven't provided formulas for f and g. ans = f(x)*diff(g(x), x) + g(x)*diff(f(x), x) >> diff( f(x)/g(x) ) ans = diff(f(x), x)/g(x) - (f(x)*diff(g(x), x))/g(x)^2 >> diff( f(x)/g(x), 2 ) ans = diff(f(x), x, x)/g(x) - (2*diff(f(x), x)*diff(g(x), x))/g(x)^2 + (2*f(x)*diff(g(x), x)^2)/g(x)^3 - (f(x)*diff(g(x), x, x))/g(x)^2 >> diff( x^n ) ans = n*x^(n - 1)
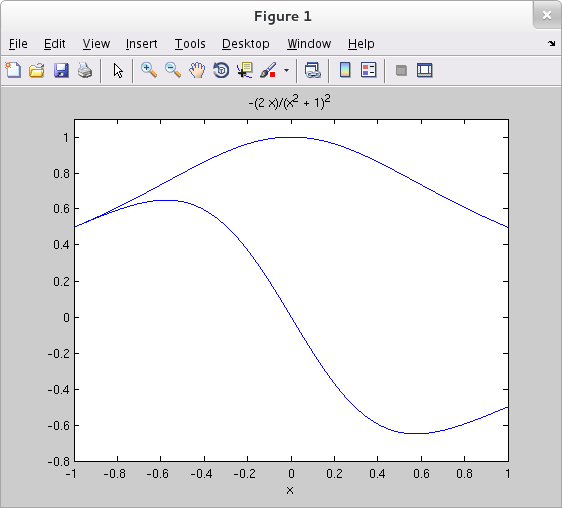
Symbolic expressions can be graphed directly with ezplot().
>> syms x y >> y = 1/(1+x^2); >> yp = diff(y); >> ezplot(y, [-1 1]) >> syms x y >> y = 1/(1+x^2); >> yp = diff(y); >> ezplot(y, [-1 1]) >> hold on >> ezplot(yp, [-1 1]) >> axis([-1 1 -.8 1.1])

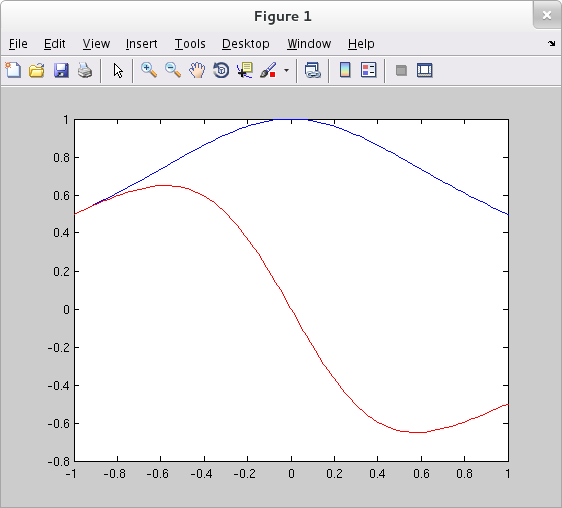
The subs() command may be employed to perform numerical computations according to symbolic formulas.
>> syms x y >> y = 1/(1+x^2); >> yp = diff(y); >> xx = linspace(-1,1,100); >> yy = subs(y,x,xx); % Substitute the numerical values in xx for variable x in symbolic expression y, compute and store results in yy. >> yyp = subs(yp,x,xx); >> plot(xx,yy,'b',xx,yyp,'r')
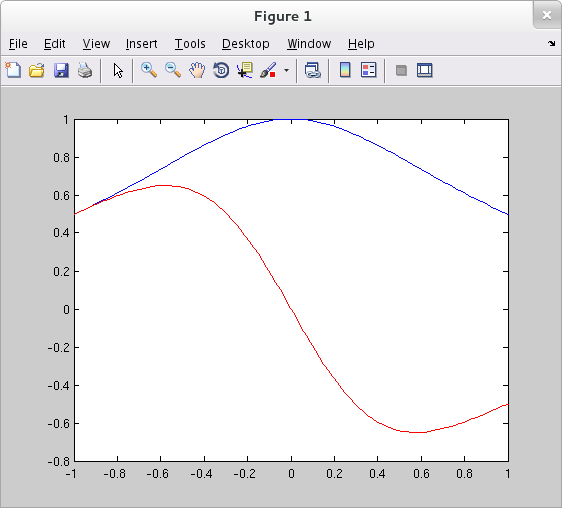
Symbolic expressions may be converted to function handles with matlabFunction().
>> syms x y >> y = 1/(1+x^2); >> yp = diff(y); >> x = linspace(-1,1,100); >> y = matlabFunction(y) % Convert symbolic expression to a MATLAB function y = @(x)1.0./(x.^2+1.0) >> y = y(x); % Apply function to numerical values stored in x. >> yp = matlabFunction(yp) yp = @(x)x.*1.0./(x.^2+1.0).^2.*-2.0 >> yp = yp(x); >> plot(x,y,'b',x,yp,'r')
Mathematica's D[] operator performs symbolic differentiation. It's first input is the expression to be differentiated. The second input is the variable with respect to which differentiation is to be performed, or a list pairing the variable of differentiation with the desired order of differentiation.

By default different symbols are considered to be independent. But a functional dependence can be asserted using square brackets.
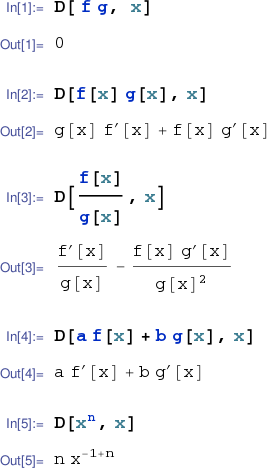
Some care is required if you wish to facilitate subsequent use of the output of D[] by naming it.
