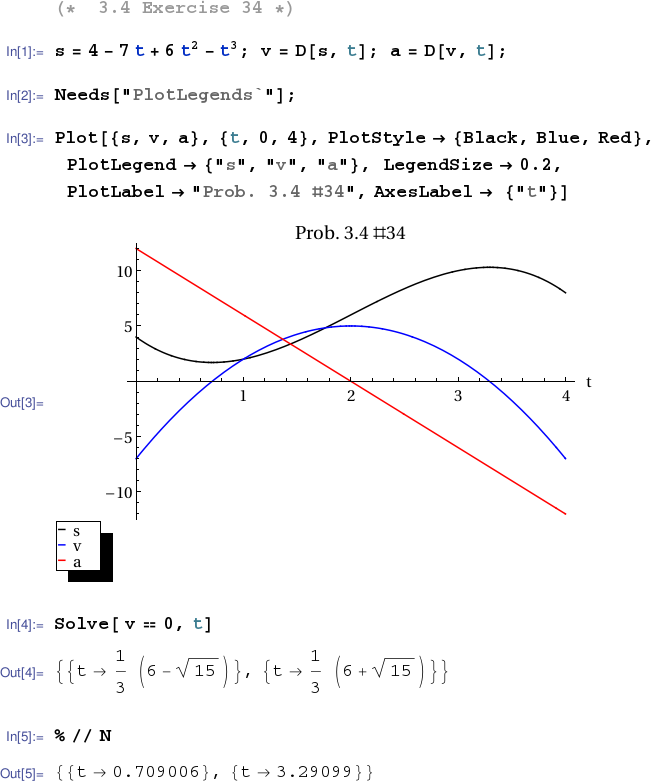
This page presents solutions in each CAS to exercise 34 from $\S$3.4.
The MATLAB code below follows a hopefully now familiar pattern. The new elements, namely the grid on command and the 'Location' option to the legend() command, are self-explanatory.
>> % Plot of position, velocity and acceleration for Prob 3.4 #34 >> t = linspace(0,4,100); >> s = 4 - 7*t + 6*t.^2 - t.^3; >> v = -7 + 12*t - 3*t.^2; >> a = 12 - 6*t; >> plot( t, s, 'k', t, v, 'b', t, a, 'r' ) >> grid on >> legend( 'position', 'velocity', 'acceleration', 'Location', 'North' ) >> title('Prob. 3.4 #34', 'FontSize', 15 )

(a) When is the object momentarily at rest?
The object is momentarily at rest when the velocity is zero. From the plot
this appears to occur at approximately $t=.7$ and $t=3.3$. For more
accurate values we can solve the quadratic equation $-3t^2+6t-7=0$
to get
$t=2\pm\frac{\sqrt{15}}{3}\approx .709, 3.291$.
(b) When does it move to the left (down) or to the right (up)?
It moves to left when $v<0$ (in this case this occurs for
$t\in[0,2-\frac{\sqrt{15}}{3})\cup(2+\frac{\sqrt{15}}{3},4]$) and right when $v>0$
(in this case when $t\in(2-\frac{\sqrt{15}}{3},2+\frac{\sqrt{15}}{3})$).
(c) When does it change direction?
It changes direction when $v$ has a transition in sign. In this example
$v$ indeed does have a sign transition at each moment when it is $0$,
namely when
$t=2\pm\frac{\sqrt{15}}{3}\approx .709, 3.291$.
(d) When does it speed up and slow down?
Speed up occurs when $v$ and $a$ have the same sign. For this example
this occurs when $t\in(2-\frac{\sqrt{15}}{3},2)\cup(2+\frac{\sqrt{15}}{3},4]$.
Slow down occurs when $v$ and $a$ have opposite signs. Here for
$t\in[0,2-\frac{\sqrt{15}}{3})\cup(2,2+\frac{\sqrt{15}}{3})$.
(e) When is it moving fastest (highest speed)? Slowest?
It's moving fastest when $|v|$ is largest. For the interval in question
this occurs at the initial and final moments $t=0$ and $t=4$.
(Note that at $t=2$ the object is moving faster than at any sufficiently
nearby time. So we may say that speed achieves a local or relative max
at $t=2$. But this is not the maximum speed attained for
the time interval $[0,4]$.) The object is at it's slowest when it
is momentarily at rest. See (a).
(f) When is it farthest from the axis origin?
It is farthest from the axis origin at $t=2+\frac{\sqrt{15}}{3}$.
(It is not a coincidence that this is one of the moments at which
the object is momentarily at rest.)
Since it's very easy to differentiate low degree polynomials with small integer coefficients by hand, there was no need to use MATLAB's symbolic differentiation capabilities for this problem. However, we could if we wanted to. The code below would produce the same plot as above.
>> syms t s v a >> s = 4 - 7*t + 6*t^2 - t^3; >> v = diff(s); >> a = diff(v); >> tt = linspace(0,4,100); >> ss = subs(s,t,tt); >> vv = subs(v,t,tt); >> aa = subs(a,t,tt); >> plot( tt, ss, 'k', tt, vv, 'b', tt, aa, 'r' ) >> grid on >> legend( 'position', 'velocity', 'acceleration', 'Location', 'North' ) >> title('Prob. 3.4 #34', 'FontSize', 15 )
Here's the plot in Mathematica. For answers to the questions (a)-(f) see the Octave/MATLAB section above.