This page demonstrates the syntax for computing one-sided limits in each of our target CASs. The names for the greatest integer and least integer functions are also introduced for each CAS.
MATLAB's symbolic toolbox computes one-sided limits using fairly transparent syntax as illustrated below.
>> syms x >> limit( sqrt( exp(x)-x-1 ) / x, x, 0, 'right' ) ans = 2^(1/2)/2 >> limit( sqrt( exp(x)-x-1 ) / x, x, 0, 'left' ) ans = -2^(1/2)/2
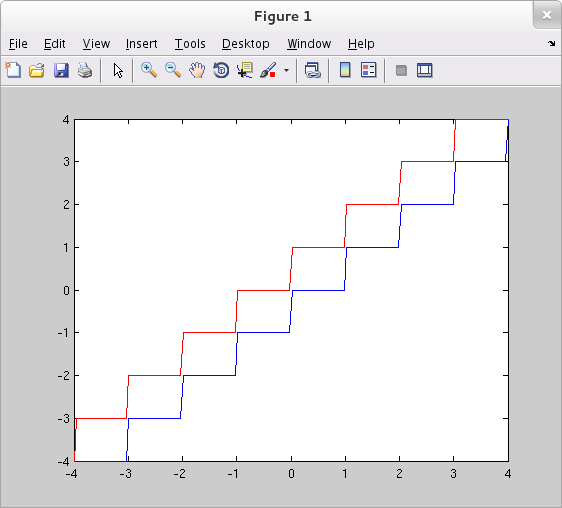
The greatest integer and least integer functions are implemented in MATLAB (and Octave) as floor() and ceil(), respectively.
>> x = linspace( -4, 4, 200 ); >> y1 = floor(x); >> y2 = ceil(x); >> plot( x, y1, 'b', x, y2, 'r' );


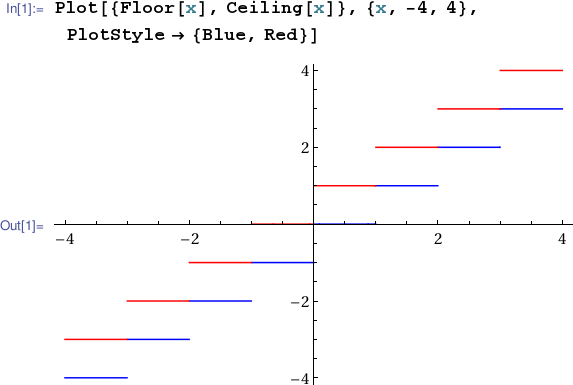
The greatest integer function $\lfloor\bullet\rfloor: \mathbb{R}\rightarrow\mathbb{Z}$ defined by setting $\lfloor x \rfloor$ equal to the greatest integer less than or equal to $x$ is implemented in Mathematica as Floor[]. The least integer function $\lceil\bullet\rceil: \mathbb{R}\rightarrow\mathbb{Z}$ defined by setting $\lceil x \rceil$ equal to the least integer greater than or equal to $x$ is implemented as Ceiling[]. For integer values of $x$, Floor[x] = Ceiling[x] = x. Otherwise, x-1 < Floor[x] < x < Ceiling[x] = Floor[x]+1 < x+1.
The direction of approach in a Sage limit() computation may be specified by setting the dir option.
The greatest integer and least integer functions are implemented in Sage as floor() and ceil(), respectively.